6 Lesson 2b: Model evaluation & selection

The last couple of lessons gave you a good introduction to building predictive models using the tidymodels construct. This lesson is going to go deeper into the idea of model evaluation & selection. We’ll discuss how to incorporate cross-validation procedures to give you a more robust assessment of model performance. We’ll also discuss the concept of hyperparameter tuning, the bias-variance tradeoff, and how to implement a tuning strategy to find a model the maximizes generalizability.

6.1 Learning objectives

By the end of this lesson you will be able to:

  1. Perform cross-validation procedures for more robust model performance assessment.
  2. Execute hyperparameter tuning to find optimal model parameter settings.

6.2 Prerequisites

For this lesson we’ll use several packages provided via tidymodels and we’ll use the ames housing data. However, for this module we’ll use the Ames housing data provided by the AmesHousing package.

Take a minute to check out the Ames data from AmesHousing::make_ames(). It is very similar to the Ames data provided in the CSV. Note that the various quality/condition variables (i.e. Overall_Qual) are already encoded as ordinal factors. 

library(tidymodels)

ames <- AmesHousing::make_ames()

Let’s go ahead and create our train-test split:

# create train/test split
set.seed(123)  # for reproducibility
split  <- initial_split(ames, prop = 0.7)
train  <- training(split)
test   <- testing(split)

6.3 Resampling & cross-validation

In the previous lessons we split our data into training and testing sets and we assessed the performance of our model on the test set. Unfortunately, there are a few pitfalls to this approach:

  1. If our dataset is small, a single test set may not provide realistic expectations of our model’s performance on unseen data.
  2. A single test set does not provide us any insight on variability of our model’s performance.
  3. Using our test set to drive our model building process can bias our results via data leakage.

Resampling methods provide an alternative approach by allowing us to repeatedly fit a model of interest to parts of the training data and test its performance on other parts of the training data.

Illustration of resampling.

Figure 6.1: Illustration of resampling.

This allows us to train and validate our model entirely on the training data and not touch the test data until we have selected a final “optimal” model.

The two most commonly used resampling methods include k-fold cross-validation and bootstrap sampling. This lesson focuses on using k-fold cross-validation.

6.4 K-fold cross-validation

Cross-validation consists of repeating the procedure such that the training and testing sets are different each time. Generalization performance metrics are collected for each repetition and then aggregated. As a result we can get an estimate of the variability of the model’s generalization performance.

k-fold cross-validation (aka k-fold CV) is a resampling method that randomly divides the training data into k groups (aka folds) of approximately equal size.

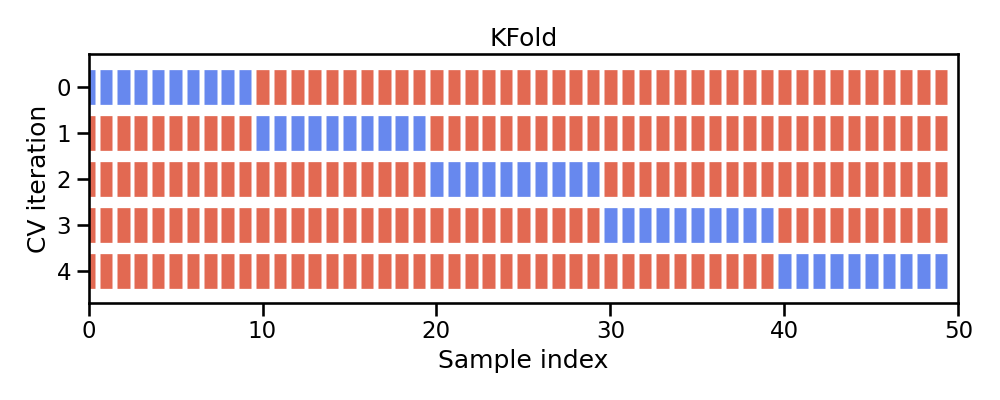
Illustration of k-fold sampling across a data sets index.

Figure 6.2: Illustration of k-fold sampling across a data sets index.

The model is fit on \(k-1\) folds and then the remaining fold is used to compute model performance. This procedure is repeated k times; each time, a different fold is treated as the validation set. Consequently, with k-fold CV, every observation in the training data will be held out one time to be included in the assessment/validation set. This process results in k estimates of the generalization error (say \(\epsilon_1, \epsilon_2, \dots, \epsilon_k\)). Thus, the k-fold CV estimate is computed by averaging the k test errors, providing us with an approximation of the error we might expect on unseen data.

Illustration of a 5-fold cross validation procedure.

Figure 6.3: Illustration of a 5-fold cross validation procedure.

In practice, one typically uses k=5 or k=10. There is no formal rule as to the size of k; however, as k gets larger, the difference between the estimated performance and the true performance to be seen on the test set will decrease.

To implement k-fold CV we first make a resampling object. In this example we create a 10-fold resampling object.

kfolds <- vfold_cv(train, v = 10)

We can now create our random forest model object and create a workflow object as we did in the previous lesson. To fit our model across our 10-folds we just use fit_resamples().

# create our random forest model object
rf_mod <- rand_forest() %>%
   set_mode('regression')

# add model object and our formula spec to a workflow object
rf_wflow <- workflow() %>% 
   add_model(rf_mod) %>%
   add_formula(Sale_Price ~ .)

# fit our model across the 10-fold CV
rf_fit_cv <- rf_wflow %>%
   fit_resamples(kfolds)

We can then get our average 10-fold cross validation error with collect_metrics():

collect_metrics(rf_fit_cv)
## # A tibble: 2 × 6
##   .metric .estimator      mean     n   std_err .config             
##   <chr>   <chr>          <dbl> <int>     <dbl> <chr>               
## 1 rmse    standard   25978.       10 898.      Preprocessor1_Model1
## 2 rsq     standard       0.902    10   0.00787 Preprocessor1_Model1

If we want to see the model evaluation metric (i.e. RMSE) for each fold we just need to unnest the rf_fit_cv object.

We have not discussed nested data frames but you can read about them here 

rf_fit_cv %>% 
   unnest(.metrics) %>%
   filter(.metric == 'rmse')
## # A tibble: 10 × 7
##    splits             id     .metric .estimator .estimate .config              .notes  
##    <list>             <chr>  <chr>   <chr>          <dbl> <chr>                <list>  
##  1 <split [1845/206]> Fold01 rmse    standard      26210. Preprocessor1_Model1 <tibble>
##  2 <split [1846/205]> Fold02 rmse    standard      22089. Preprocessor1_Model1 <tibble>
##  3 <split [1846/205]> Fold03 rmse    standard      30512. Preprocessor1_Model1 <tibble>
##  4 <split [1846/205]> Fold04 rmse    standard      26106. Preprocessor1_Model1 <tibble>
##  5 <split [1846/205]> Fold05 rmse    standard      25095. Preprocessor1_Model1 <tibble>
##  6 <split [1846/205]> Fold06 rmse    standard      24337. Preprocessor1_Model1 <tibble>
##  7 <split [1846/205]> Fold07 rmse    standard      23586. Preprocessor1_Model1 <tibble>
##  8 <split [1846/205]> Fold08 rmse    standard      30650. Preprocessor1_Model1 <tibble>
##  9 <split [1846/205]> Fold09 rmse    standard      27256. Preprocessor1_Model1 <tibble>
## 10 <split [1846/205]> Fold10 rmse    standard      23935. Preprocessor1_Model1 <tibble>

6.5 Hyperparameter tuning

Say you have the below relationship between a response variable and some predictor variable x (gray dots). Given two different models fit to this relationship (blue line), which model do you prefer?

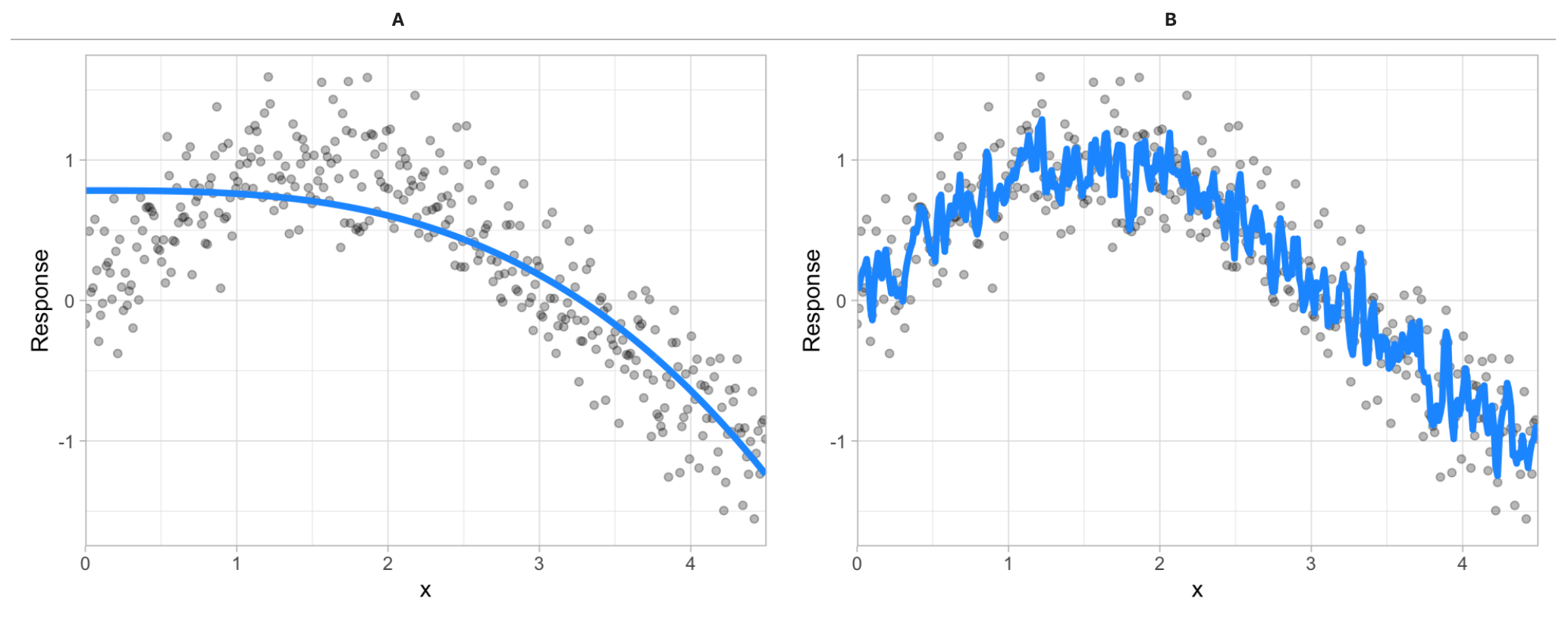
Between model A and B, which do you think is better?

Figure 6.4: Between model A and B, which do you think is better?

The image above illustrates the fact that prediction errors can be decomposed into two main subcomponents we care about:

  • error due to “bias”
  • error due to “variance”

Understanding how different sources of error lead to bias and variance helps us improve the data fitting process resulting in more accurate models.

6.5.1 Bias

Error due to bias is the difference between the expected (or average) prediction of our model and the correct value which we are trying to predict. It measures how far off in general a model’s predictions are from the correct value, which provides a sense of how well a model can conform to the underlying structure of the data.

The left image below illustrates an example where a polynomial model does not capture the underlying relationship well. Linear models are classical examples of high bias models as they are less flexible and rarely capture non-linear, non-monotonic relationships.

We also need to think of bias-variance in relation to resampling. Models with high bias are rarely affected by the noise introduced by resampling. If a model has high bias, it will have consistency in its resampling performance as illustrated by the right plot below.

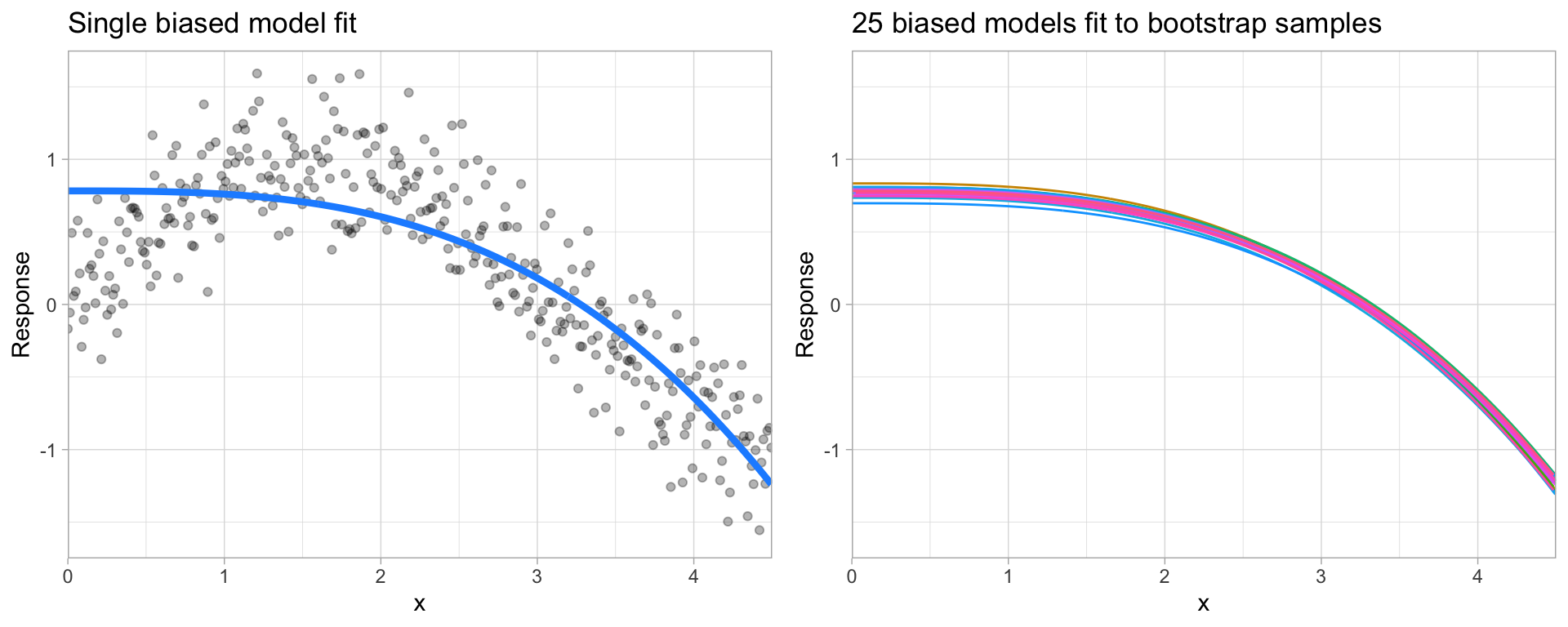
A biased polynomial model fit to a single data set does not capture the underlying non-linear, non-monotonic data structure (left). Models fit to 25 bootstrapped replicates of the data are underterred by the noise and generates similar, yet still biased, predictions (right).

Figure 6.5: A biased polynomial model fit to a single data set does not capture the underlying non-linear, non-monotonic data structure (left). Models fit to 25 bootstrapped replicates of the data are underterred by the noise and generates similar, yet still biased, predictions (right).

6.5.2 Variance

Error due to variance is the variability of a model prediction for a given data point.

Many models (e.g., k-nearest neighbor, decision trees, gradient boosting machines) are very adaptable and offer extreme flexibility in the patterns that they can fit to. However, these models offer their own problems as they run the risk of overfitting to the training data. Although you may achieve very good performance on your training data, the model will not automatically generalize well to unseen data.

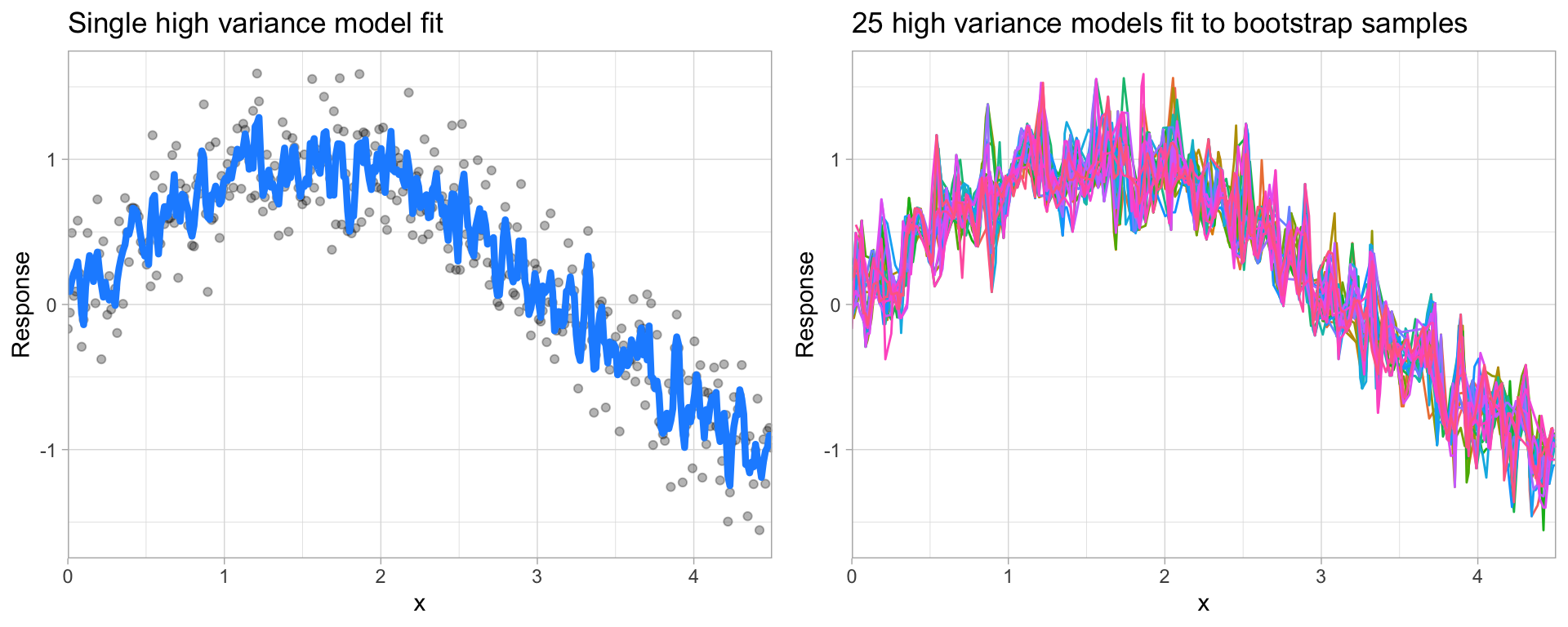
A high variance _k_-nearest neighbor model fit to a single data set captures the underlying non-linear, non-monotonic data structure well but also overfits to individual data points (left). Models fit to 25 bootstrapped replicates of the data are deterred by the noise and generate highly variable predictions (right).

Figure 6.6: A high variance k-nearest neighbor model fit to a single data set captures the underlying non-linear, non-monotonic data structure well but also overfits to individual data points (left). Models fit to 25 bootstrapped replicates of the data are deterred by the noise and generate highly variable predictions (right).

Since high variance models are more prone to overfitting, using resampling procedures are critical to reduce this risk. Moreover, many algorithms that are capable of achieving high generalization performance have lots of hyperparameters that control the level of model complexity (i.e., the tradeoff between bias and variance).

Many high performing models (i.e. random forests, gradient boosting machines, deep learning) are very flexible in the patterns they can conform to due to the many hyperparameters they have. However, this also means they are prone to overfitting (aka can have high variance error).

6.5.3 Hyperparameters

Hyperparameters (aka tuning parameters) are the “knobs to twiddle” to control the complexity of machine learning algorithms and, therefore, the bias-variance trade-off. Not all algorithms have hyperparameters (e.g., ordinary least squares8); however, most have at least one or more.

Some models have very few hyperparameters. For example, k-nearest neighbor models have a single hyperparameter (k) that determines the predicted value to be made based on the k nearest observations in the training data to the one being predicted. If k is small (e.g., \(k = 3\)), the model will make a prediction for a given observation based on the average of the response values for the 3 observations in the training data most similar to the observation being predicted. This often results in highly variable predicted values because we are basing the prediction (in this case, an average) on a very small subset of the training data. As k gets bigger, we base our predictions on an average of a larger subset of the training data, which naturally reduces the variance in our predicted values (remember this for later, averaging often helps to reduce variance!).

The plot below illustrates this point. Smaller k values (e.g., 2, 5, or 10) lead to high variance (but lower bias) and larger values (e.g., 150) lead to high bias (but lower variance). The optimal k value might exist somewhere between 20–50, but how do we know which value of k to use?

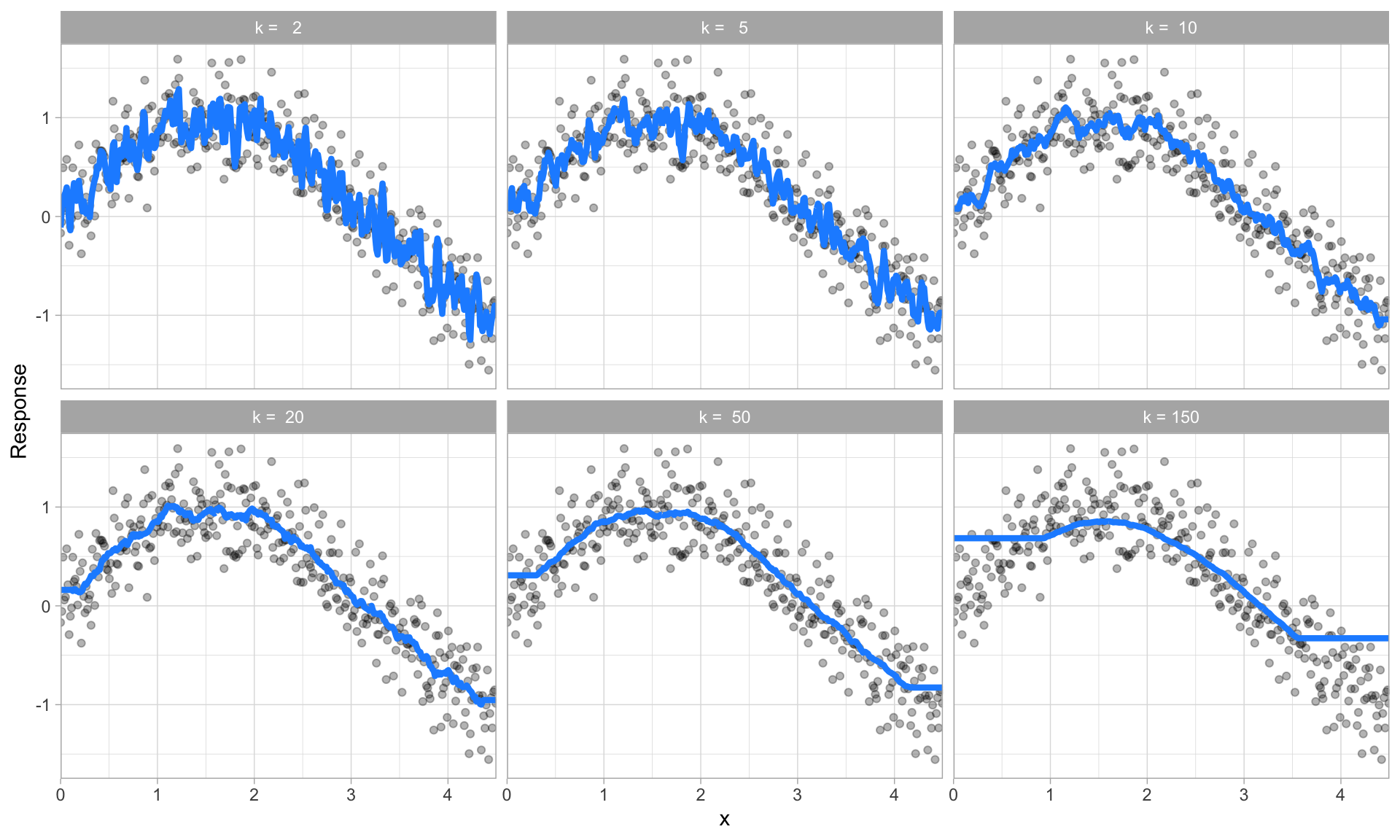
_k_-nearest neighbor model with differing values for _k_.

Figure 6.7: k-nearest neighbor model with differing values for k.

Some algorithms such as ordinary least squares don’t have any hyperparameters. Some algorithms such as k-nearest neighbor have one or two hyperparameters. And some algorithms such as gradient boosted machines (GBMs) and deep learning models have many.

Hyperparameter tuning is the process of screening hyperparameter values (or combinations of hyperparameter values) to find a model that balances bias & variance so that the model generalizes well to unseen data.

Let’s illustrate by using decision trees. One of the key hyperparameters in decision trees is the depth of the tree.

This lesson does not dig into the decision tree algorithm but if you want to better understand the hyperparameters for decision trees you can read about them here

Say we wanted to assess what happens when we grow the decision tree 5 levels deep. We could do this manually:

# create our decision tree model object
dt_mod <- decision_tree(tree_depth = 5) %>%
   set_mode('regression')

# add model object and our formula spec to a workflow object
dt_wflow <- workflow() %>% 
   add_model(dt_mod) %>%
   add_formula(Sale_Price ~ .)

# fit our model across the 10-fold CV
dt_fit_cv <- dt_wflow %>%
   fit_resamples(kfolds)

# assess results
collect_metrics(dt_fit_cv)
## # A tibble: 2 × 6
##   .metric .estimator      mean     n   std_err .config             
##   <chr>   <chr>          <dbl> <int>     <dbl> <chr>               
## 1 rmse    standard   39175.       10 1382.     Preprocessor1_Model1
## 2 rsq     standard       0.758    10    0.0156 Preprocessor1_Model1

But what if we wanted to assess and compare different tree_depth values. Moreover, decision trees have another key hyperparameter cost_complexity. So what if we wanted to assess a few values of that hyperaparameter in combination with tree_depth? Adjusting these values manually would be painstakingly burdensome.

Again, don’t worry if you have no idea what these hyperparameters mean. Just realize we want to toggle these values to try find an optimal model.

6.6 Finalizing our model

If we are satisfied with our results and we want to use the best hyperparameter values for our best decision tree model, we can select it with select_best():

# select best model based on RMSE metric
best_tree <- dt_grid_search %>%
   select_best(metric = 'rmse')

best_tree
## # A tibble: 1 × 3
##   cost_complexity tree_depth .config             
##             <dbl>      <int> <chr>               
## 1    0.0000000001          8 Preprocessor1_Model4

We can then update (or “finalize”) our workflow object dt_wflow with the values from select_best().

final_wflow <- dt_wflow %>%
   finalize_workflow(best_tree)

Finally, let’s fit this final model to the training data and use our test data to estimate the model performance we expect to see with new data. We can use the function last_fit() with our finalized model; this function fits the finalized model on the full training data set and evaluates the finalized model on the testing data.

We pass the initial train-test split object we created at the beginning of this lesson to last_fit. 

final_fit <- final_wflow %>%
   last_fit(split)

final_fit %>%
   collect_predictions() %>%
   rmse(truth = Sale_Price, estimate = .pred)
## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard      34609.

As we can see our test RMSE is less than our CV RMSE. This indicates that we did not overfit during our tuning procedure, which is a good thing.

Perhaps we would also like to understand what variables are important in this final model. We can use the vip package to estimate variable importance based on the model’s structure.

Don’t worry, we’ll talk about vip more later on and just how this measure of importance is computed. 

library(vip)

final_fit %>% 
   extract_fit_parsnip() %>% 
   vip()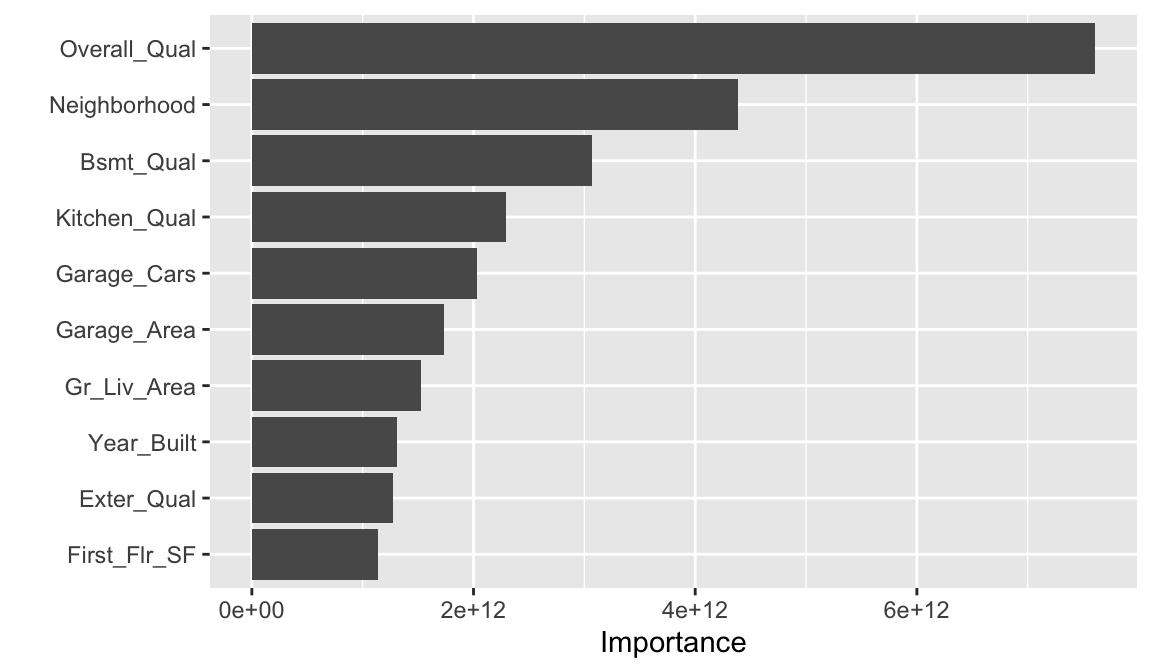

6.7 Exercises

Import the dataset blood_transfusion.csv:

  1. The column “Class” contains the target variable. Investigate this variable. Is this a regression or classification problem?
  2. Why is it relevant to add a preprocessing step to standardize the features? What step_xxx() function would you use to do so?
  3. Perform a k-nearest neighbor model on this data with neighbors = 10. Be sure to add a preprocessing step to standardize the features.
  4. Perform a 5-fold cross validation with the above model workflow. What is your average CV score?
  5. Now perform hyperparameter tuning to understand the effect of the parameter neighbors on the model score. Assess 10 values for neighbors between the range of 1-100. Again, perform a 5-fold cross validation. Which hyperparameter value performed the best and what was the CV score?

6.8 Additional resources

This module provided a very high-level introduction to predictive modeling with tidymodels. To build on this knowledge you can find many great resources at https://www.tidymodels.org/.