7 Lesson 2b: Data types & structures

Until now, you’ve created fairly simple data in R and stored it as a vector! However, when wrangling data we often come across a variety of data types and require different data structures to manage them. This lesson serves to introduce you to the basic data types and structures in R that you’ll most commonly use.

7.1 Learning objectives

Upon completing this module you will be able to:

• Explain the difference between data types and data structures.
• Identify what data types you are working with in R and convert data types if necessary.
• Create different data structures, perform indexing to extract items from the different data structures and apply operators on data structures.

7.2 Data types

R has six basic types of data: numeric, integer, logical, character, complex and raw. However, it is very unlikely that in your time as a data analyst/scientist you’ll need to work with complex and raw data types so we’ll focus on the first four.

• Numeric data are numbers that contain a decimal. Actually they can also be whole numbers but we’ll gloss over that.

• Integers are whole numbers (those numbers without a decimal point).

• Logical data take on the value of either TRUE or FALSE. There’s also another special type of logical called NA to represent missing values.

• Character data are used to represent string values. You can think of character strings as something like a word (or multiple words). A special type of character string is a factor, which is a string but with additional attributes (like levels or an order). We’ll cover factors later.

7.2.1 Determining the type

R is (usually) able to automatically distinguish between different classes of data by their nature and the context in which they’re used although you should bear in mind that R can’t actually read your mind and you may have to explicitly tell R how you want to treat a data type. You can find out the type (or class) of any object using the class() function.

num <- 2.2
class(num)
## [1] "numeric"

char <- "hello world"
class(char)
## [1] "character"

logi <- TRUE
class(logi)
## [1] "logical"

Alternatively, you can ask if an object is a specific class using a logical test. The is.xxxx() family of functions will return either a TRUE or a FALSE.

is.numeric(num)
## [1] TRUE

is.character(num)
## [1] FALSE

is.character(char)
## [1] TRUE

is.logical(logi)
## [1] TRUE

7.2.2 Type conversion

It can sometimes be useful to be able to change the class of a variable using the as.xxxx() family of coercion functions, although you need to be careful when doing this as you might receive some unexpected results (see what happens below when we try to convert a character string to a numeric).

# coerce numeric to character
class(num)
## [1] "numeric"

num_char <-  as.character(num)
num_char
## [1] "2.2"

class(num_char)
## [1] "character"

# coerce character to numeric!
class(char)
## [1] "character"

char_num <- as.numeric(char)
## Warning: NAs introduced by coercion

Functions to test and and coerce data types.

Type	Logical test	Coercing
Character	is.character	as.character
Numeric	is.numeric	as.numeric
Logical	is.logical	as.logical
Factor	is.factor	as.factor
Complex	is.complex	as.complex

In later modules we will learn how to wrangle these different data types plus other special data types that are built on top of these classes (i.e. date-time stamps, missing values). For now, I just want you to understand the foundational data types built into R.

7.2.3 Knowledge check

1. Check out the built-in object pi. What class is this object?
2. What happens when you coerce this object to a character?
3. What happens when you coerce it to a logical?
4. Is there a coercion function that could convert this to an integer? What happens when you do this?

7.3 Data structures

Now that you’ve been introduced to some of the most important classes of data in R, let’s have a look at some of main structures that we have for storing these data.

7.3.1 Scalars and vectors

Perhaps the simplest type of data structure is the vector. You’ve already been introduced to vectors in module 1. Vectors that have a single value (length 1) are often referred to as scalars. Vectors can contain numbers, characters, factors or logicals, but the key thing to remember is that all the elements inside a vector must be of the same class. In other words, vectors can contain either numbers, characters or logicals but not mixtures of these types of data. There is one important exception to this, you can include NA (this is special type of logical) to denote missing data in vectors with other data types.

All the elements inside a vector must be of the same class

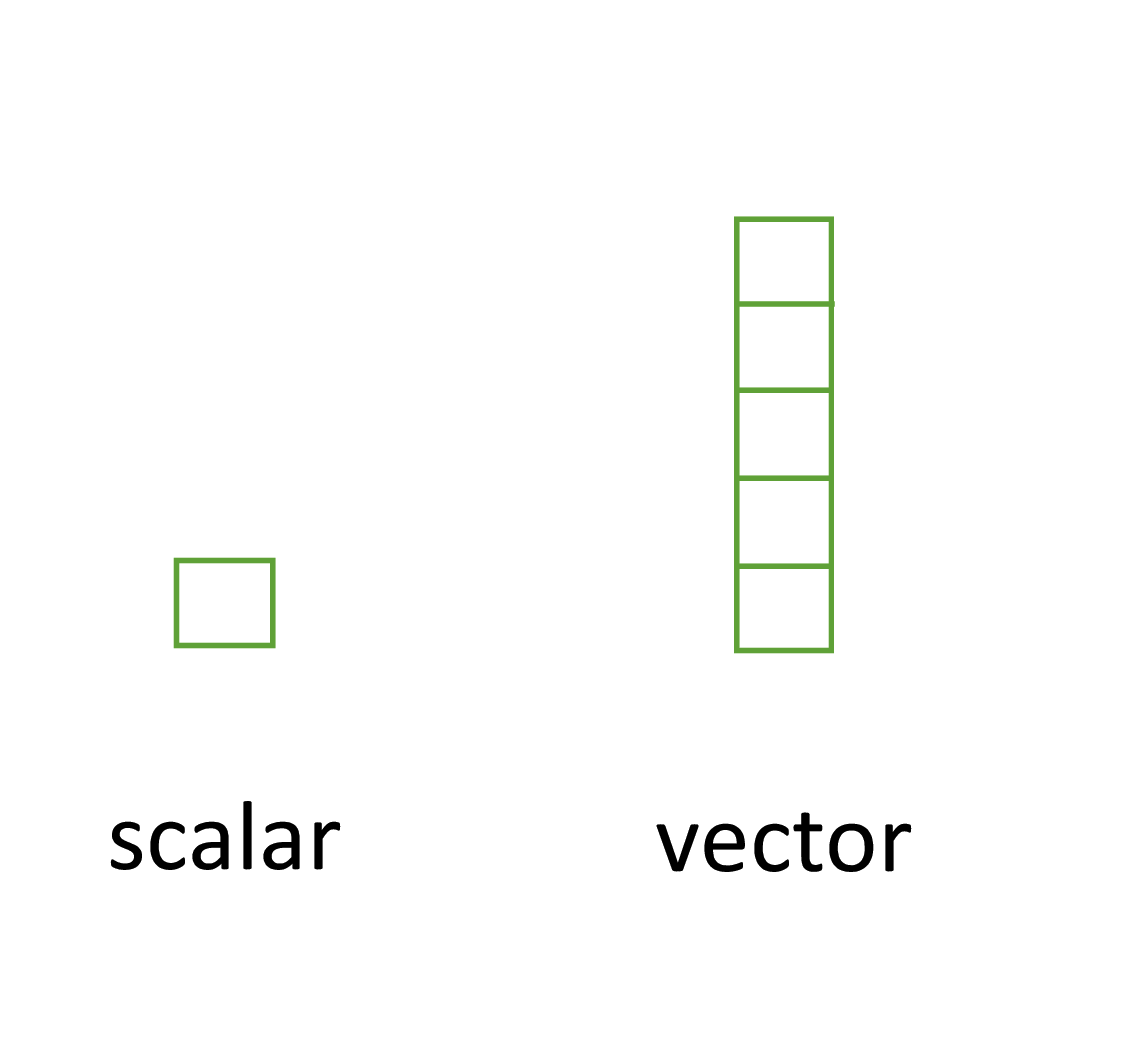
Figure 7.1: Scalars versus vectors. In R, the only difference is the number of elements.

7.3.2 Matrices and arrays

Another useful data structure used in many disciplines such as population ecology, theoretical and applied statistics is the matrix. A matrix is simply a vector that has additional attributes called dimensions. Arrays are just multidimensional matrices. Again, matrices and arrays must contain elements all of the same data class.

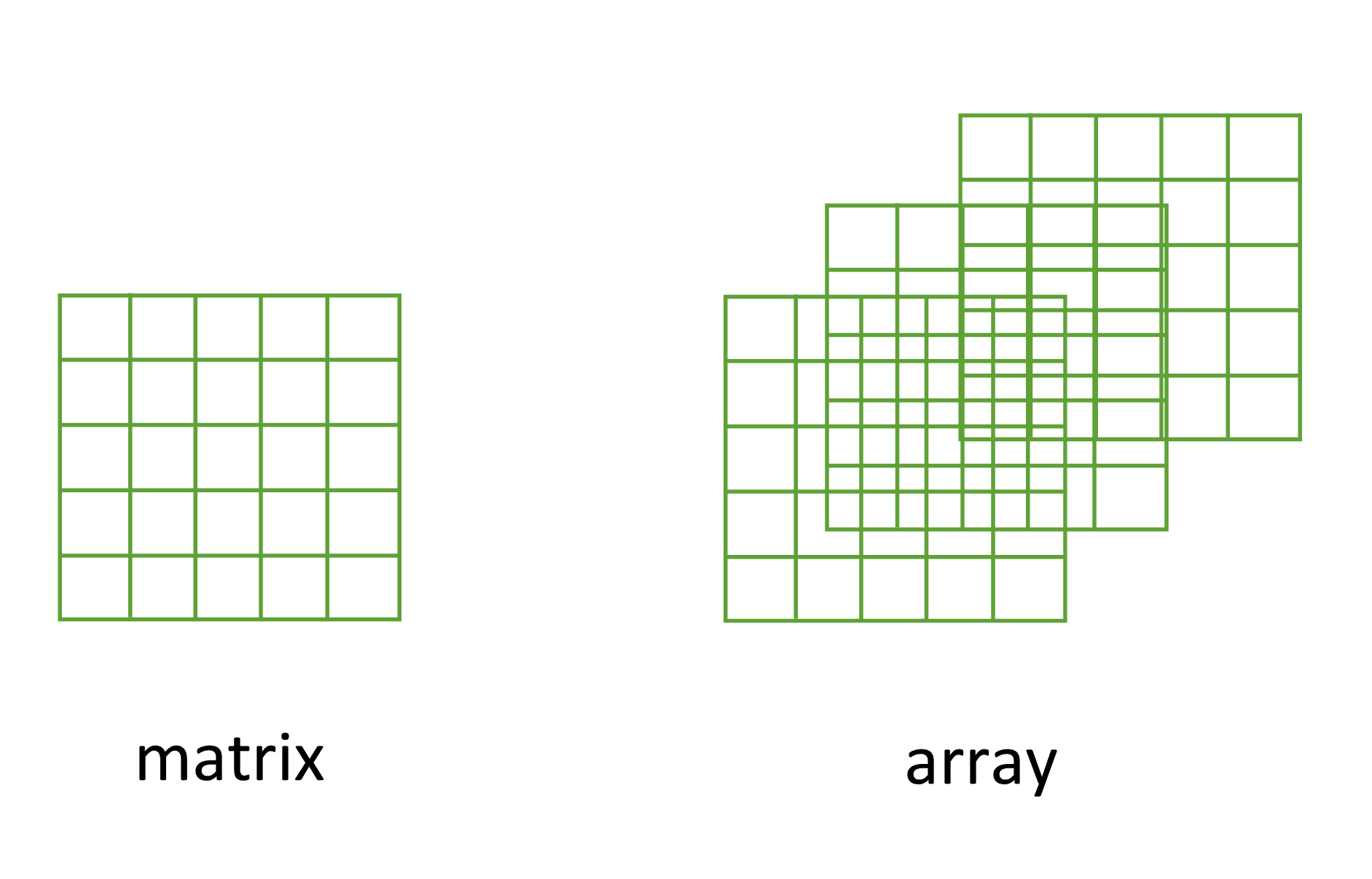
Figure 7.2: Matrices versus arrays.

7.3.2.1 Creating

A convenient way to create a matrix or an array is to use the matrix() and array() functions respectively. Below, we will create a matrix from a sequence 1 to 16 in four rows (nrow = 4) and fill the matrix row-wise (byrow = TRUE) rather than the default column-wise. When using the array() function we define the dimensions using the dim = argument, in our case 2 rows, 4 columns in 2 different matrices.

my_mat <- matrix(1:16, nrow = 4, byrow = TRUE)
my_mat
##      [,1] [,2] [,3] [,4]
## [1,]    1    2    3    4
## [2,]    5    6    7    8
## [3,]    9   10   11   12
## [4,]   13   14   15   16
my_array <- array(1:16, dim = c(2, 4, 2))
my_array
## , , 1
## 
##      [,1] [,2] [,3] [,4]
## [1,]    1    3    5    7
## [2,]    2    4    6    8
## 
## , , 2
## 
##      [,1] [,2] [,3] [,4]
## [1,]    9   11   13   15
## [2,]   10   12   14   16

Sometimes it’s also useful to define row and column names for your matrix but this is not a requirement. To do this use the rownames() and colnames() functions.

rownames(my_mat) <- c("A", "B", "C", "D")
colnames(my_mat) <- c("a", "b", "c", "d")
my_mat
##    a  b  c  d
## A  1  2  3  4
## B  5  6  7  8
## C  9 10 11 12
## D 13 14 15 16

7.3.2.2 Indexing

Similar to vectors, we can extract elements from our matrix using [] notation. The main difference is we now have to specify two dimensions in our indexing matrix[row, col]:

# element located at the intersection of the 
# third row and second column
my_mat[3, 2]
## [1] 10

We can also leave one dimension empty if we want to retrieve all elements for that particular dimension.

# all elements in the second row
my_mat[2, ]
## a b c d 
## 5 6 7 8

# all elements in the third column
my_mat[, 3]
##  A  B  C  D 
##  3  7 11 15

And when rows and columns are named we can also index based on those names:

# Element located in row 'A' and column 'b'
my_mat['A', 'b']
## [1] 2

7.3.2.3 Operators

Once you’ve created your matrices you can do useful stuff with them and as you’d expect. Many of the functions we used in the vector lesson can be applied across an entire matrix:

# mean of all elements
mean(my_mat)
## [1] 8.5

However, there are also unique functions that work on matrices but not vectors. For example, we can compute the mean of each column in a matrix:

colMeans(my_mat)
##  a  b  c  d 
##  7  8  9 10

R has numerous built in functions to perform matrix operations. Some of the most common are given below. For example, to transpose a matrix we use the transposition function t():

my_mat_t <- t(my_mat)
my_mat_t
##   A B  C  D
## a 1 5  9 13
## b 2 6 10 14
## c 3 7 11 15
## d 4 8 12 16

To extract the diagonal elements of a matrix and store them as a vector we can use the diag() function:

my_mat_diag <- diag(my_mat)
my_mat_diag
## [1]  1  6 11 16

The usual matrix addition, multiplication etc can be performed. Note the use of the %*% operator to perform matrix multiplication.

mat.1 <- matrix(c(2, 0, 1, 1), nrow = 2)    
mat.1
##      [,1] [,2]
## [1,]    2    1
## [2,]    0    1

mat.2 <- matrix(c(1, 1, 0, 2), nrow = 2)
mat.2
##      [,1] [,2]
## [1,]    1    0
## [2,]    1    2

mat.1 + mat.2           # matrix addition
##      [,1] [,2]
## [1,]    3    1
## [2,]    1    3
mat.1 * mat.2           # element by element products
##      [,1] [,2]
## [1,]    2    0
## [2,]    0    2
mat.1 %*% mat.2     # matrix multiplication
##      [,1] [,2]
## [1,]    3    2
## [2,]    1    2

7.3.2.4 Knowledge check

1. Check out the built-in VADeaths data matrix?
2. Subset this matrix for only male death rates.
3. Subset for males death rates over the age of 60.
4. Calculate averages for each column and row.

7.3.3 Lists

The next data structure we will quickly take a look at is a list. Whilst vectors and matrices are constrained to contain data of the same type, lists are able to store mixtures of data types. In fact we can even store other data structures such as vectors and arrays within a list or even have a list of a list.

Lists a very flexible data structures which is ideal for storing irregular or non-rectangular data. Many statistical outputs are provided as a list as well; therefore, its critical to understand how to work with lists.

7.3.3.1 Creating

To create a list we can use the list() function. Note how each of the three list elements are of different classes (character, logical, and numeric) and are of different lengths.

list_1 <- list(c("black", "yellow", "orange"),
               c(TRUE, TRUE, FALSE, TRUE, FALSE, FALSE),
               matrix(1:6, nrow = 3))
list_1
## [[1]]
## [1] "black"  "yellow" "orange"
## 
## [[2]]
## [1]  TRUE  TRUE FALSE  TRUE FALSE FALSE
## 
## [[3]]
##      [,1] [,2]
## [1,]    1    4
## [2,]    2    5
## [3,]    3    6

Elements of the list can be named during the construction of the list

list_2 <- list(colours = c("black", "yellow", "orange"), 
               evaluation = c(TRUE, TRUE, FALSE, TRUE, FALSE, FALSE), 
               time = matrix(1:6, nrow = 3))
list_2
## $colours
## [1] "black"  "yellow" "orange"
## 
## $evaluation
## [1]  TRUE  TRUE FALSE  TRUE FALSE FALSE
## 
## $time
##      [,1] [,2]
## [1,]    1    4
## [2,]    2    5
## [3,]    3    6

or after the list has been created using the names() function

names(list_1) <- c("colors", "evaluation", "time")
list_1
## $colors
## [1] "black"  "yellow" "orange"
## 
## $evaluation
## [1]  TRUE  TRUE FALSE  TRUE FALSE FALSE
## 
## $time
##      [,1] [,2]
## [1,]    1    4
## [2,]    2    5
## [3,]    3    6

We can always get a quick glimpse of the structure of a list using str():

str(list_1)
## List of 3
##  $ colors    : chr [1:3] "black" "yellow" "orange"
##  $ evaluation: logi [1:6] TRUE TRUE FALSE TRUE FALSE FALSE
##  $ time      : int [1:3, 1:2] 1 2 3 4 5 6

7.3.3.2 Indexing

To subset lists we can utilize the single bracket [ ], double brackets [[ ]], and dollar sign $ operators. Each approach provides a specific purpose and can be combined in different ways to achieve the following subsetting objectives:

• Subset list and preserve output as a list
• Subset list and simplify output
• Subset list to get elements out of a list

To extract one or more list items while preserving the output in list format use the [ ] operator.

Its important to understand the difference between simplifying and preserving subsetting. Simplifying subsets returns the simplest possible data structure that can represent the output. Preserving subsets keeps the structure of the output the same as the input. See Hadley Wickham’s section on Simplifying vs. Preserving Subsetting to learn more.

# extract first list item
list_1[1]
## $colors
## [1] "black"  "yellow" "orange"

# same as above but using the item's name
list_1['colors']
## $colors
## [1] "black"  "yellow" "orange"

# extract multiple list items
list_1[c('colors', 'time')]
## $colors
## [1] "black"  "yellow" "orange"
## 
## $time
##      [,1] [,2]
## [1,]    1    4
## [2,]    2    5
## [3,]    3    6

To extract one or more list items while simplifying the output use the [[ ]] or $ operator:

# extract first list item
list_1[[1]]
## [1] "black"  "yellow" "orange"

# same as above but using the item's name
list_1[['colors']]
## [1] "black"  "yellow" "orange"

# same as above but using $
list_1$colors
## [1] "black"  "yellow" "orange"

One thing that differentiates the [[ operator from the \(</code> is that the <code>[[</code> operator can be used with computed indices. The <code>\) operator can only be used with literal names.

To extract individual elements out of a specific list item combine the [[ (or $) operator with the [ operator:

# extract the third element of the first list item
list_1[['colors']][3]
## [1] "orange"

7.3.3.3 Operators

There are less operators that you typically use directly on a list. Most of the time you are trying to extract items out of a list. However, a few useful functions that are applied to a list include:

# how many items are in a list
length(list_1)
## [1] 3

# the name of the list items
names(list_1)
## [1] "colors"     "evaluation" "time"

# the overall structure of a list
str(list_1)
## List of 3
##  $ colors    : chr [1:3] "black" "yellow" "orange"
##  $ evaluation: logi [1:6] TRUE TRUE FALSE TRUE FALSE FALSE
##  $ time      : int [1:3, 1:2] 1 2 3 4 5 6

7.3.3.4 Knowledge check

Install and load the nycflights13 package:

install.packages('nycflights13')

Using the flights data provided by this package create the following regression model:

This line of code is performing a linear regression model and saving the results in a list called flight_lm. We’ll discuss linear regression and modeling in later modules.

flight_lm <- lm(arr_delay ~ dep_delay + month + carrier, data = flights)

1. How many items are in this list?
2. What are the names of these list items?
3. Extract the coefficients of this model.
4. Extract the departure delay (dep_delay) coefficient.

7.3.4 Data frames

By far the most commonly used data structure to store data is the data frame. A data frame is a powerful two-dimensional object made up of rows and columns which looks superficially very similar to a matrix. However, whilst matrices are restricted to containing data all of the same type, data frames can contain a mixture of different types of data. Typically, in a data frame each row corresponds to an individual observation and each column corresponds to a different measured or recorded variable. This setup may be familiar to those of you who use Microsoft Excel to manage and store your data. Perhaps a useful way to think about data frames is that they are essentially made up of a bunch of vectors (columns) with each vector containing its own data type but the data type can be different between vectors.

As an example, the data frame below contains total quantity and sales for a grocery product category (i.e. potatoes, popcorn, frozen pizza) for each household. The data frame has four variables (columns) and each row represents an individual household. The variables household_id, total_quantity, and total_sales are numeric, product_category is a character, and multiple_items is a Boolean representing if the household bought more than one item.

Table 7.1: Sample data frame

household_id	product_category	total_quantity	total_sales	multiple_items
1129	CONDIMENTS/SAUCES	1	0.89	FALSE
1136	NEWSPAPER	1	1.50	FALSE
1450	FD WRAPS/BAGS/TRSH BG	1	2.49	FALSE
2334	MAGAZINE	3	10.47	TRUE
2341	SOFT DRINKS	5	5.30	TRUE
2406	COLD CEREAL	1	2.99	FALSE
420	FLUID MILK PRODUCTS	1	1.00	FALSE
493	SALD DRSNG/SNDWCH SPRD	1	2.50	FALSE
788	BABY HBC	1	1.37	FALSE
842	SOFT DRINKS	11	14.66	TRUE

There are a couple of important things to bear in mind about data frames. These types of objects are known as rectangular data as each column must have the same number of observations. Also, any missing data should be recorded as an NA just as we did with our vectors.

7.3.4.1 Creating

Data frames are usually created by reading in a data set, which we’ll cover in a later lesson. However, data frames can also be created explicitly with the data.frame() function or they can be coerced from other types of objects like lists. In this case I’ll create a simple data frame df and assess its basic structure:

df <- data.frame(col1 = 1:3, 
                 col2 = c("this", "is", "text"), 
                 col3 = c(TRUE, FALSE, TRUE), 
                 col4 = c(2.5, 4.2, pi))

# assess the structure of a data frame
str(df)
## 'data.frame':    3 obs. of  4 variables:
##  $ col1: int  1 2 3
##  $ col2: chr  "this" "is" "text"
##  $ col3: logi  TRUE FALSE TRUE
##  $ col4: num  2.5 4.2 3.14

# number of rows
nrow(df)
## [1] 3

# number of columns
ncol(df)
## [1] 4

We can also convert pre-existing structures to a data frame. The following illustrates how we can turn multiple vectors into a data frame:

v1 <- 1:3
v2 <-c("this", "is", "text")
v3 <- c(TRUE, FALSE, TRUE)

# convert same length vectors to a data frame using data.frame()
data.frame(col1 = v1, col2 = v2, col3 = v3)
##   col1 col2  col3
## 1    1 this  TRUE
## 2    2   is FALSE
## 3    3 text  TRUE

7.3.4.2 Indexing

Data frames possess the characteristics of both lists and matrices: if you index with a single vector, they behave like lists and will return the selected columns with all rows; if you subset with two vectors, they behave like matrices and can be subset by row and column:

df
##   col1 col2  col3   col4
## 1    1 this  TRUE 2.5000
## 2    2   is FALSE 4.2000
## 3    3 text  TRUE 3.1416

# subsetting by row numbers
df[2:3, ]
##   col1 col2  col3   col4
## 2    2   is FALSE 4.2000
## 3    3 text  TRUE 3.1416

# subsetting by row names
df[c("row2", "row3"), ]
##      col1 col2 col3 col4
## NA     NA <NA>   NA   NA
## NA.1   NA <NA>   NA   NA

# subset for both rows and columns
df[1:2, c(1, 3)]
##   col1  col3
## 1    1  TRUE
## 2    2 FALSE

You can also subset data frames based on conditional statements. To illustrate we’ll use the built-in mtcars data frame:

head(mtcars)
##                    mpg cyl disp  hp drat    wt  qsec vs am gear carb
## Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
## Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
## Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
## Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1
## Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2
## Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1

# all rows where mpg is greater than 20
mtcars[mtcars$mpg > 20, ]
##                 mpg cyl  disp  hp drat    wt  qsec vs am gear carb
## Mazda RX4      21.0   6 160.0 110 3.90 2.620 16.46  0  1    4    4
## Mazda RX4 Wag  21.0   6 160.0 110 3.90 2.875 17.02  0  1    4    4
## Datsun 710     22.8   4 108.0  93 3.85 2.320 18.61  1  1    4    1
## Hornet 4 Drive 21.4   6 258.0 110 3.08 3.215 19.44  1  0    3    1
## Merc 240D      24.4   4 146.7  62 3.69 3.190 20.00  1  0    4    2
## Merc 230       22.8   4 140.8  95 3.92 3.150 22.90  1  0    4    2
## Fiat 128       32.4   4  78.7  66 4.08 2.200 19.47  1  1    4    1
## Honda Civic    30.4   4  75.7  52 4.93 1.615 18.52  1  1    4    2
## Toyota Corolla 33.9   4  71.1  65 4.22 1.835 19.90  1  1    4    1
## Toyota Corona  21.5   4 120.1  97 3.70 2.465 20.01  1  0    3    1
## Fiat X1-9      27.3   4  79.0  66 4.08 1.935 18.90  1  1    4    1
## Porsche 914-2  26.0   4 120.3  91 4.43 2.140 16.70  0  1    5    2
## Lotus Europa   30.4   4  95.1 113 3.77 1.513 16.90  1  1    5    2
## Volvo 142E     21.4   4 121.0 109 4.11 2.780 18.60  1  1    4    2

Its good to know that we can index and filter data frames in this fashion but later lessons will demonstrate an alternative, and more common approach to wrangle data frames. In fact, most of the lessons that follow are all focused on working with data frames!

7.4 Exercises

1. Check out the built-in mtcars data set. What type of object is this?
2. Apply the head() and summary() functions to mtcars, what do these functions return?
3. Index for just the ‘mpg’ column in mtcars using three different approaches: single brackets ([), double brackets [[, and dollar sign $. How do the results differ?
4. Use one of the methods in #3 to save the ‘mpg’ column as a vector. Now compute the mean of this vector.